Trojčlenka
Trojčlenka je matematický úkon, jehož pomocí se počítají přímé a nepřímé úměry ve slovních úlohách.
Trojčlenku často používáme i v běžném životě, aniž bychom si to uvědomovali, např. při počítání procent.
Při počítání pomocí trojčlenky většinou známe tři na sobě závislé údaje a potřebujeme vypočítat čtvrtý. Vždy je zároveň důležité vědět, jestli se jedná o přímou či nepřímou úměru, neboť každá se počítá jinak.
Jak se počítá trojčlenka
Pro výpočet trojčlenky existuje jednoduchý zápis:
X ……… Y
x ……… y
kdy [X], [x] a [Y] jsou známé údaje a [y] je neznámá, kterou potřebujeme vypočítat.
U přímé úměry pak výpočet vypadá takto:
x / X = y / Y
y = x · Y / X
U nepřímé úměry vypadá výpočet takto:
X / x = y / Y
y = X · Y / x
Na názorných příkladech si ukážeme rozdíl mezi přímou a nepřímou úměrou a ukážeme si, jak se trojčlenka počítá.
Přímá úměra u trojčlenky a příklady
U přímé úměry si můžeme říci „čím více…, tím více“ nebo „čím méně…, tím méně“. Např.:
- Čím více lidí bude sázet stromky, tím více jich vysadí.
- Čím méně budu mít peněz, tím méně zmrzliny si mohu koupit.
- Čím větší bude nádrž, tím více vody se do ní vejde.
Příklad trojčlenky: Za dvě hodiny jsem ujel 150 km. Jak dlouho mi bude trvat ujet 450 km? (Přímá úměra – čím déle jedu, tím více ujedu.)
Postup: Napíšeme si, co víme, pomocí tohoto zápisu:
150 km (X) ……… 2 hod (Y)
↑ 450 km (x) ……… x hod (y) ↑
Jelikož se jedná o přímou úměru, nakreslím si na obě strany šipku nahoru a počítám:
450 / 150 = x / 2
x = 2 · 450 / 150
x = 6
Výsledek tedy je, že 450 km ujedu za 6 hodin.
Nepřímá úměra u trojčlenky a příklady
U nepřímé úměry si můžeme říci „čím více…, tím méně“ nebo „čím méně…, tím více“. Např.:
- Čím více montážníků bude dům stavět, tím méně času jim to zabere.
- Čím méně peněz utratím, tím více mi jich zbyde.
- Čím rychleji pojedu, tím méně času pojedu do cíle.
Příklad trojčlenky: Ve dvou postavíme dům za 15 měsíců. Za jak dlouho dům postavíme, když nás bude pět? (Nepřímá úměra – čím více lidí staví, tím méně času jim to zabere.)
Postup: Napíšeme si, co víme, pomocí tohoto zápisu:
2 lidi (X) ……… 15 měsíců (Y)
↓ 5 lidí (x) ……… x měsíců (y) ↑
Jelikož se jedná o nepřímou úměru, vpravo napíšeme šipku nahoru a vlevo dolů. Šipka u neznámého údaje míří vždy nahoru (respektive od neznámého údaje ke známému). Výpočet trojčlenky:
2 / 5 = x / 15
x = 2 · 15 / 5
x = 6
Výsledek je, že 5 lidí bude dům stavět 6 měsíců.
Online kalkulačka pro výpočet trojčlenky
Naše online kalkulačka vám snadno a rychle vypočítá chybějící údaj. Do políček vepište známé údaje podle vzoru příkladů výše a zvolte, zda se jedná o přímou, či nepřímou úměru. Údaje vepište pouze číselně, bez jednotek.
Vyplňte tři políčka:
| → | ||
| → | ||
Související kalkulačky
Výpočet procent
Rychlý a jednoduchý online výpočet procent. Výpočet procenta z celku nebo rozdíl mezi čísly v procentech.Cena dřevostavby
Výpočet ceny dřevostavby a doby návratnosti vyššího energetického standarduCena řeziva
Výpočet ceny řeziva podle průřezu a objemu profilu nebo podle jeho ceny za běžný metr.Výpočet DPH
Výpočet DPH ze zadané ceny, výpočet ceny s DPH a bez DPH. Pracuje se všemi sazbami.Úhlopříčka čtverce výpočet
Potřebujete vypočítat úhlopříčku čtverce? Bezplatná online kalkulačka i vzorec na této stránce.Převody jednotek hmotnosti
Online kalkulačka na převody jednotek hmotnosti. Snadno a rychle si provedete převody hmotnosti mezi všemi běžnými jednotkami.Objem válce výpočet
Potřebujete vypočítat objem válce? Použijte tento rychlý a jednoduchý online výpočet obsahu válce. Výsledek je možné zobrazit ve všech jednotkách.Hmotnost dřeva
Výpočet hmotnosti 1 m3 dřeva na základě druhu a vlhkosti dřeviny.Další zajímavé články o dřevostavbách

Lidé si začali montovat fotovoltaiku sami, aby ušetřili. Pak ale neseženou revizi a nesmí ji používat
Vysoké ceny energií a tlak na úspory přivádějí stále více lidí k úvaze o pořízení vlastní fotovoltaické elektrárny. Touha vyrábět si elektřinu doma a snížit účty je pochopitelná...
Váš názor na tuto kalkulačku
- Vypočítejte si trojčlenku snadno a rychle pomocí online kalkulačky.
- Pro výpočet trojčlenky stačí znát vstupní hodnoty.
- Nezapomeňte zvolit, zda se jedná o přímou, či nepřímou úměru.
- Trojčlenka se hodí např. pro výpočet procent.
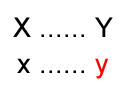
NOVINKY E-MAILEM ZDARMA
Přihlaste se k odběru a dostávejte nejžhavější novinky:
